How To Find The Inverse Of A 2x2 Matrix

The inverse of a 2x2 matrix

In our past lesson nosotros learnt that for an invertible matrix there is always another matrix which multiplied to the first, will produce the identity matrix of the same dimensions as them.
In other words, an invertible matrix is that which has an changed matrix related to it, and if both of them (the matrix and its inverse) are multiplied together (no thing in which club), the upshot will exist an identity matrix of the aforementioned gild. In full general, the condition of invertibility for a nxn matrix $A$ is:

A \cdot A^{-1}=A^{-one}A \cdot A =I_{n}

Equation 1: Full general condition for matrix A to be invertible

Therefore, if we define a 2x2 matrix $X,$ the condition for the inverse 2x2 matrix is written as:

X \cdot X^{-1} =Ten^{-ane} \cdot X=I_{2}

Equation 2: Condition for matrix 10 to be invertible

But how do yous detect the inverse of a 2x2 matrix? Nosotros become through the whole process to discover the inverse of a 2x2 matrix in our showtime section for this lesson, and so we follow that concept past making the calculations which show it is right in the second section. And then go set up and lets have some math fun!

How to find the inverse of a 2x2 matrix

In social club to know what is the inverse of a 2x2 matrix we must offset by defining a second order matrix, such as matrix $Ten$ shown beneath:

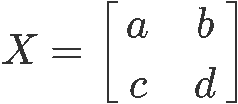
Solving systems of linear equations by graphing

Equation 3: Matrix Ten

From our lesson on the the determinant of a 2x2 matrix we learnt that the determinant of $10$ is mathematically defined as:

det (10)=advertisement-bc

Equation iv: Determinant of matrix Ten

Now we need to find its matrix changed $X^{-1}$ . When thinking on the expression $X^{-one}$ the first idea that comes to mind is a division since an exponent of minus 1 in general algebra denotes a division of one past the number that has the exponent. The problem is that the operation of division using matrices does non be given that a matrix is not a detail value, but a collection or assortment of multiple values, which geometrically speaking, do not even represent values in the same dimensional plane (depending on the dimensions of the matrix itself), so partition by such a range of different variable characteristics cannot be defined and so we say that matrix division is undefined.
This is where the concept of inversion comes to play an important role, then, although not sectionalization per se, a matrix inversion comes to stand for a related performance which will let you to abolish out matrices when solving systems of equations or even simple matrix multiplications.

The formula for the changed of a 2x2 matrix $X$ is divers as:

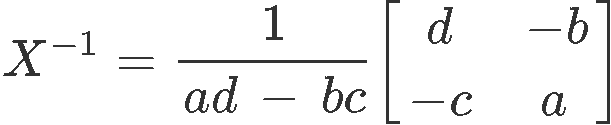
Equation 5: Formula for the inverse of a 2x2 matrix

Detect that the outset cistron in the right hand side equanimous by a division of one past a subtraction of the multiplication of the matrix elements, is equal to take a factor of ane divided past the determinant of the matrix. In afterwards lessons you lot will see how this detail factor occurs in full general in the formula for the inverse matrix of whatever size of matrices.

For now, we continue to focus on the changed of a 2x2 matrix and the next question arises: Why is an inverse matrix important, and how can it be used?

Imagine you have a matrix multiplication defined equally $A \cdot B = C$ , where all $A$ , $B$ , and $C$ are square matrices of the same order (same dimensions) and $A$ and $C$ are both known. Then you are asked to find out what the $B$ matrix is.
Intuitively you will call back about dividing out matrix $A$ from both sides of the equation in club to cancel it out from the left hand side and solve for $B$ ; this is the method that we would use if they were regular variables after all, the problem is, these are matrices and partition of matrices does not exist! What practise we do? We obtain the inverse of matrix $A$ and multiply information technology to both sides of the equation:

A \cdot B = C

A^{-one} \cdot A \cdot B=A^{-ane} \cdot C

I_{n} \cdot B=A^{-1} \cdot C

B=A^{-1} \cdot C

Equation 6: Solving for matrix B

This particular solution allows u.s. to observe how the inversion of matrices is the equivalent to divide one by a matrix, and thus, how it can be used to cancel out matrices in equations which require a division. We have been able to solve for matrix $B$ in equation 6 thanks to use our knowledge from equation 1: the multiplication of a matrix and its inverse, no matter in which order the factors are arranged, produces an identity matrix $I_{n}$ of the same dimensions equally the original matrices. And then, applying what nosotros learnt in our lesson nigh the identity matrix, nosotros know that any matrix multiplied by an identity matrix gives a result the non-identity matrix itself. And so, we tin can conclude that $B$ is equal to the changed of $A$ fourth dimension $C$ .

Having learnt the usage and how to get the inverse of a 2x2 matrix, let us go next into a department dedicated to show that equations 2 and 5 are correct, if other words, let u.s.a. calculate the inverse of 2x2 matrix proof with an instance given matrix so yous can find the formula for changed of 2x2 matrix in action. Later, in our last department, we will piece of work through a series of exercises in guild for you to practice.

Inverse of a 2x2 matrix proof

On this department nosotros will prove how a 2x2 matrix and its inverse come across the condition defined in equation ii. For that we define matrix $A$ as shown below:

Equation 7: Matrix A

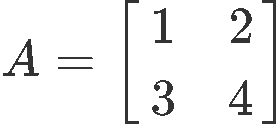
The starting time function of our proof is to verify this matrix is in fact an invertible matrix, for that, we obtain its determinant:

Equation 8: Determinant of A

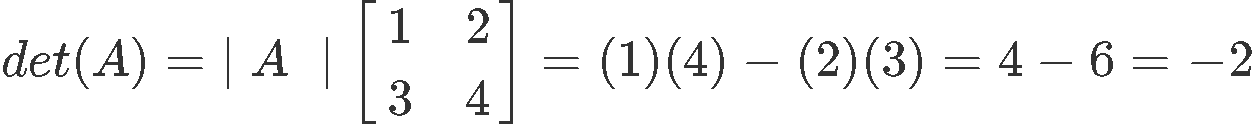
Since our matrix $A$ has a determinant which is non equal to zero, we tin determine $A$ is an invertible matrix and so, we can finally calculate its inverse. For that, we utilise equation 5 and obtain:

Equation ix: Changed matrix of A

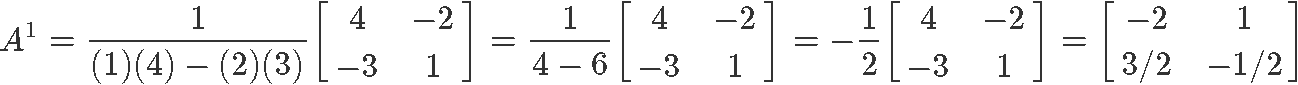
Hence, now we can finally testify the expression found in equation 2 by multiplying matrix $A$ with is inverse.

Equation x: Proving the status of invertibility of A

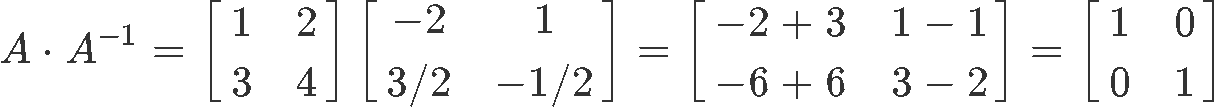
And and so, as you lot can see, the matrix multiplication between matrix $A$ and its inverse produces the identity matrix with the same dimensions equally them. Therefore we accept proved that the expressions providing the conditions for invertibility of a matrix (shown in both equation one and equation 2), hold true.

Remember the expression found in equation 1 provides de invertibility condition in general, meaning, it applies to square matrices of any order (dimensions). In later lessons we volition look at how to compute the changed of 3x3 matrices with matrix row operations. Notice nosotros have non used row operations during the adding of a 2x2 inverse, and so, why trying it with a dissimilar method when the matrix gets a lilliputian bigger?

The reason is that we could utilise a process to find the inverse of a larger matrix based on the same principle as the one we are using today for a 2x2 matrix (which would also comprise a gene of one over the determinant of the matrix), BUT, as the original matrix gets bigger, such procedure becomes too large and time consuming to be practical. And so, we volition be looking into a method using row operations because nosotros believe is a much more practical approach.

For at present, we volition continue to focus on the inverse of 2x2 matrices only, then allow us go along.

Exercise problems for finding the inverse of a 2x2 matrix

Example 1

Using the matrices $X$ and $Y$ provided below:

Equation 11: Matrices Ten and Y

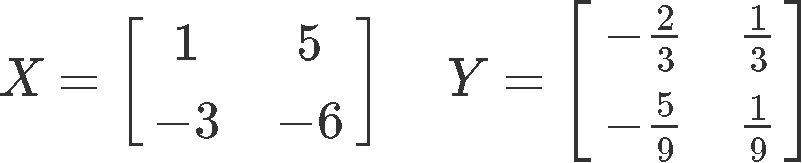
Bank check if the two matrices are inverses.
We attack this problem by remembering that 2 matrices are inverses of each other they will produce an identity matrix of their same dimensions when being multiplied, just equally described in equation ii for the example of 2x2 matrices. Therefore, allow us employ that expression and multiply matrices $X$ and $Y$ in order to run across what they produce:

Equation 12: Multiplying 10 and Y

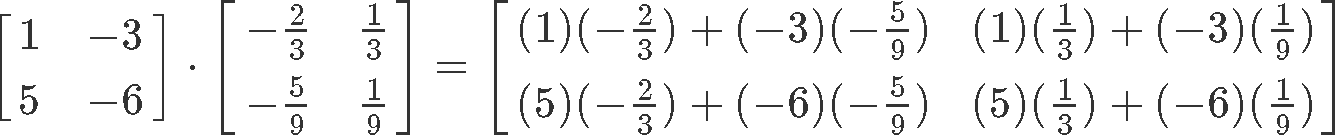
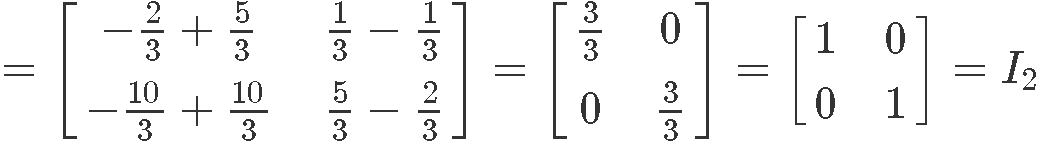
Every bit you tin encounter, the product of matrices $X$ and $Y$ happens to be the identity matrix of second order, therefore, these two matrices are inverses of each other.

Case ii

But as washed in problem example ane, use the two matrices ( $A$ and $B$ ) divers beneath and prove if they are inverses of each other.

Equation 13: Matrices A and B

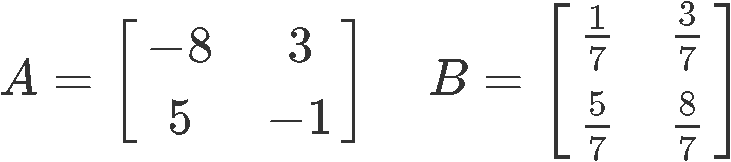
So, we multiply $A$ and $B$ :

Equation 14: Multiplying A and B

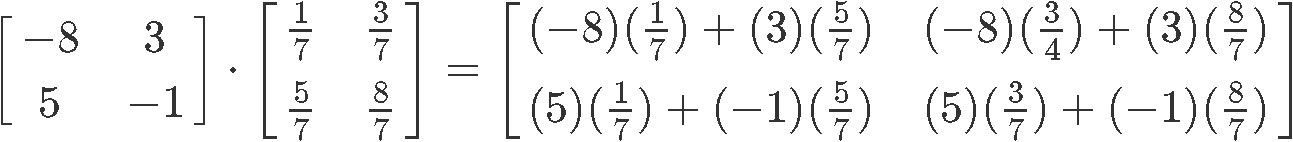
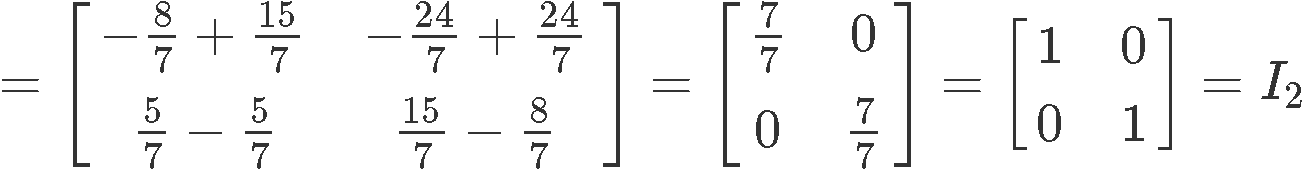
Since the production of $A$ and $B$ is an identity matrix, then that means $A$ and $B$ are two matrices inverses of each other.

Case 3

Once more than, we employ the matrices $A$ and $B$ provided below:

Equation 15: Matrices A and B

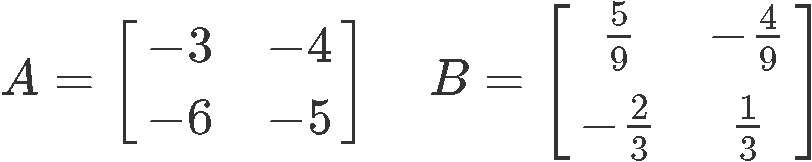
And bank check if the two matrices are inverses by multiplying them:

Equation 16: Multiplying A and B

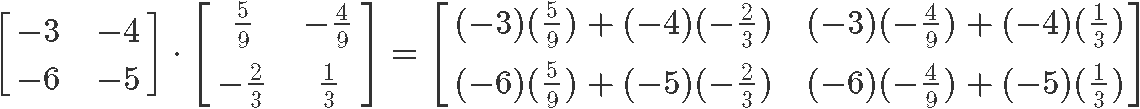
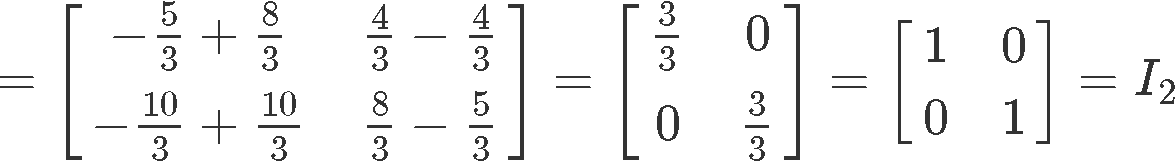
And over again, we have proved that $A$ and $B$ are inverses of each other due the identity matrix being the event of their multiplication.

Now, before we continue with some other exercises, it is of import to notation something: The order in which you multiply matrices which are inverses of each other does not make a modify on their product, their multiplication will nevertheless produce the identity matrix.Therefore, if a square matrix is invertible, the matrix multiplication of such matrix and its inverse is commutative (no thing the social club in which they are multiplied, they ever produce the same upshot: the identity). You can check this on your own and nosotros recommend that you to do it for practice.

***

For the side by side four instance exercises nosotros will be using the general formula for changed of 2x2 matrix as shown in equation five, in gild to obtain the result in each case.

Example 4

Notice the inverse of 2x2 matrix $10$ defined below:

Equation 17: Matrix X

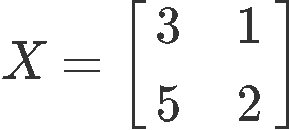
For this, as mentioned before, we utilise equation five (inverse of 2x2 matrix formula) assuming the matrix X follows the element notation from equation 3. Therefore, the computation of the 2x2 changed matrix goes every bit follows:

Equation 18: Matrix inverse of X

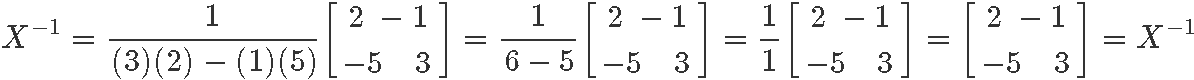
Instance five

Having matrix A as defined below:

Equation 21: Matrix F

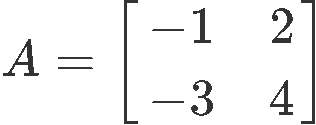
Calculate its 2x2 matrix changed:

Equation 20: Matrix inverse of A

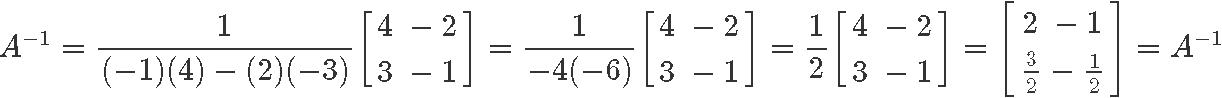
Instance 6

Calculate the matrix changed 2x2 of F, which is defined beneath:

Equation 21: Matrix F

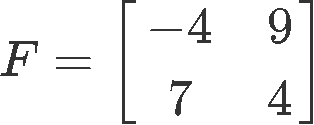
Using equation 5 nosotros obtain:

Equation 22: Matrix inverse of F

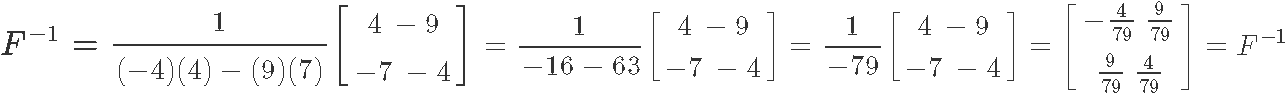
Example 7

If $C$ is defined equally the identity matrix of second social club (just as shown below). What is the changed of matrix 2x2 on this case?

Equation 23: Matrix C

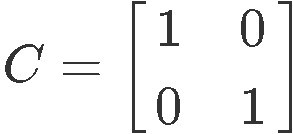
We truly practice non need to brand any calculations to answer this question since during our lesson on the 2x2 invertible matrix we learnt that the identity matrix is an involutory matrix (or just an involution for simplicity). Retrieve that an involutory matrix is that which multiplied past itself (squaring the matrix) produces the identity matrix, and then, an involutory matrix is that which is its own inverse. Therefore, we can rapidly conclude the inverse of $C$ for this case will be $C$ itself.

We have even proved this before past multiplying the 2x2 identity matrix by itself generating the identity matrix once more, such as shown hither:

Equation 24: The identity matrix as inverse multiplicative of itself.

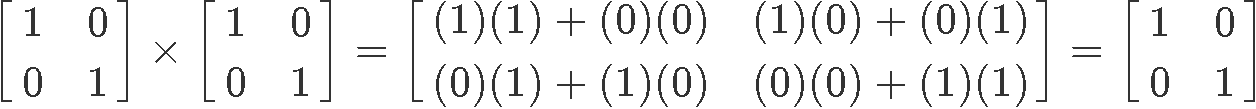
For the purpose of clarity, allow us not work the inverse using the formula for the changed of a matrix 2x2 shown in equation five so we can encounter the same result volition be obtained:

Equation 25: Matrix inverse of C

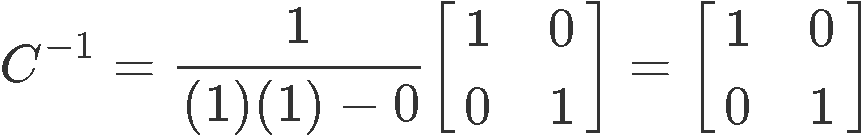
So, as predicted before, the changed of matrix 2x2 named $C$ is $C$ itself due to involution.

***

Now that we accept learnt what an invertible matrix is and how to obtain it, is time to find a use for it and that is what our next lesson is all about, then go prepare!
Before nosotros go, allow us recommend y'all an extra resource containing data and extra example exercises about inverse matrices, as well it, you could besides visit this handout on the inverse of a matrix and Cramers rule.
So, this is it for today, see yous on our next lesson!