How To Find Directional Derivative Of A Vector
Differentiation of Functions of Several Variables
26 Directional Derivatives and the Slope
Learning Objectives
- Determine the directional derivative in a given direction for a function of ii variables.
- Determine the slope vector of a given real-valued office.
- Explicate the significance of the gradient vector with regard to management of change along a surface.
- Use the gradient to find the tangent to a level bend of a given role.
- Calculate directional derivatives and gradients in three dimensions.
In Partial Derivatives we introduced the partial derivative. A function ![]() has ii fractional derivatives:
has ii fractional derivatives: ![]() and
and ![]() These derivatives correspond to each of the independent variables and can be interpreted equally instantaneous rates of change (that is, equally slopes of a tangent line). For example,
These derivatives correspond to each of the independent variables and can be interpreted equally instantaneous rates of change (that is, equally slopes of a tangent line). For example, ![]() represents the slope of a tangent line passing through a given point on the surface defined past
represents the slope of a tangent line passing through a given point on the surface defined past ![]() assuming the tangent line is parallel to the x-centrality. Similarly,
assuming the tangent line is parallel to the x-centrality. Similarly, ![]() represents the slope of the tangent line parallel to the
represents the slope of the tangent line parallel to the ![]() Now we consider the possibility of a tangent line parallel to neither axis.
Now we consider the possibility of a tangent line parallel to neither axis.
Directional Derivatives
We start with the graph of a surface defined by the equation ![]() Given a point
Given a point ![]() in the domain of
in the domain of ![]() we cull a direction to travel from that point. Nosotros mensurate the management using an angle
we cull a direction to travel from that point. Nosotros mensurate the management using an angle ![]() which is measured counterclockwise in the ten, y-plane, starting at zero from the positive 10-centrality ((Figure)). The altitude we travel is
which is measured counterclockwise in the ten, y-plane, starting at zero from the positive 10-centrality ((Figure)). The altitude we travel is ![]() and the direction we travel is given by the unit vector
and the direction we travel is given by the unit vector ![]() Therefore, the z-coordinate of the second point on the graph is given past
Therefore, the z-coordinate of the second point on the graph is given past ![]()
Finding the directional derivative at a point on the graph of ![]() The slope of the black arrow on the graph indicates the value of the directional derivative at that indicate.
The slope of the black arrow on the graph indicates the value of the directional derivative at that indicate.

We can calculate the slope of the secant line by dividing the deviation in ![]() by the length of the line segment connecting the ii points in the domain. The length of the line segment is
by the length of the line segment connecting the ii points in the domain. The length of the line segment is ![]() Therefore, the slope of the secant line is
Therefore, the slope of the secant line is
![]()
To detect the slope of the tangent line in the same management, nosotros have the limit as ![]() approaches zero.
approaches zero.
Definition
Suppose ![]() is a office of ii variables with a domain of
is a office of ii variables with a domain of ![]() Let
Let ![]() and define
and define ![]() And so the directional derivative of
And so the directional derivative of ![]() in the management of
in the management of ![]() is given by
is given by
![]()
provided the limit exists.
(Figure) provides a formal definition of the directional derivative that can be used in many cases to calculate a directional derivative.
First of all, since ![]() and
and ![]() is astute, this implies
is astute, this implies
![]()
Using ![]() we first summate
we first summate ![]()
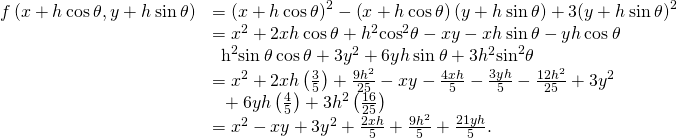
Nosotros substitute this expression into (Effigy):
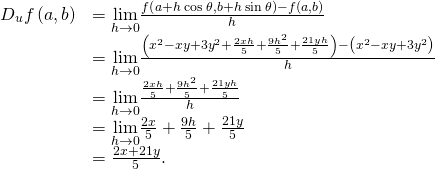
To summate ![]() we substitute
we substitute ![]() and
and ![]() into this answer:
into this answer:
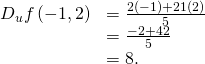
(Encounter the following figure.)
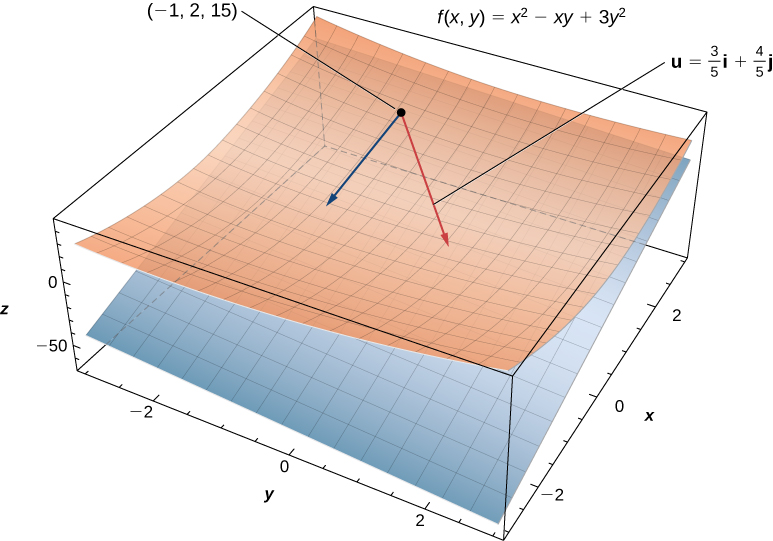
Finding the directional derivative in a given management ![]() at a given point on a surface. The aeroplane is tangent to the surface at the given bespeak
at a given point on a surface. The aeroplane is tangent to the surface at the given bespeak ![]()
Another arroyo to calculating a directional derivative involves fractional derivatives, equally outlined in the following theorem.
Proof
(Figure) states that the directional derivative of f in the direction of ![]() is given past
is given past
![]()
Let ![]() and
and ![]() and define
and define ![]() Since
Since ![]() and
and ![]() both exist, we can utilize the chain rule for functions of two variables to calculate
both exist, we can utilize the chain rule for functions of two variables to calculate ![]()
![]()
If ![]() then
then ![]() and
and ![]() so
so
![]()
Past the definition of ![]() it is as well true that
it is as well true that
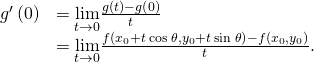
Therefore, ![]()
□
First, nosotros must calculate the partial derivatives of ![]()
![]()
Then we utilise (Figure) with ![]()
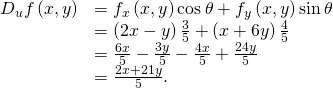
To summate ![]() let
let ![]() and
and ![]()
![]()
This is the same answer obtained in (Figure).
Find the directional derivative ![]() of
of ![]() in the direction of
in the direction of ![]() using (Figure). What is
using (Figure). What is ![]()
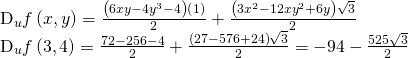
Hint
Calculate the fractional derivatives and decide the value of ![]()
If the vector that is given for the management of the derivative is not a unit vector, then it is only necessary to divide past the norm of the vector. For example, if we wished to observe the directional derivative of the function in (Figure) in the management of the vector ![]() nosotros would first divide by its magnitude to get
nosotros would first divide by its magnitude to get ![]() This gives us
This gives us ![]() And then
And then
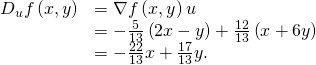
Gradient
The correct-paw side of (Effigy) is equal to ![]() which can be written as the dot product of two vectors. Define the first vector as
which can be written as the dot product of two vectors. Define the first vector as ![]() and the second vector as
and the second vector as ![]() Then the correct-mitt side of the equation can exist written equally the dot product of these two vectors:
Then the correct-mitt side of the equation can exist written equally the dot product of these two vectors:
![]()
The showtime vector in (Figure) has a special proper noun: the gradient of the function ![]() The symbol
The symbol ![]() is called nabla and the vector
is called nabla and the vector ![]() is read
is read ![]()
Finding Gradients
Find the gradient ![]() of each of the following functions:
of each of the following functions:
Notice the gradient ![]() of
of ![]()
![]()
Hint
Calculate the partial derivatives, then use (Figure).
The gradient has some of import properties. Nosotros take already seen one formula that uses the gradient: the formula for the directional derivative. Call up from The Dot Product that if the bending betwixt two vectors ![]() and
and ![]() is
is ![]() then
then ![]() Therefore, if the angle between
Therefore, if the angle between ![]() and
and ![]() is
is ![]() we have
we have
![]()
The ![]() disappears because
disappears because ![]() is a unit vector. Therefore, the directional derivative is equal to the magnitude of the gradient evaluated at
is a unit vector. Therefore, the directional derivative is equal to the magnitude of the gradient evaluated at ![]() multiplied by
multiplied by ![]() Retrieve that
Retrieve that ![]() ranges from
ranges from ![]() to
to ![]() If
If ![]() then
then ![]() and
and ![]() and
and ![]() both indicate in the same direction. If
both indicate in the same direction. If ![]() and then
and then ![]() and
and ![]() and
and ![]() point in contrary directions. In the first case, the value of
point in contrary directions. In the first case, the value of ![]() is maximized; in the second instance, the value of
is maximized; in the second instance, the value of ![]() is minimized. If
is minimized. If ![]() and so
and so ![]() for any vector
for any vector ![]() These iii cases are outlined in the post-obit theorem.
These iii cases are outlined in the post-obit theorem.
The gradient indicates the maximum and minimum values of the directional derivative at a point.
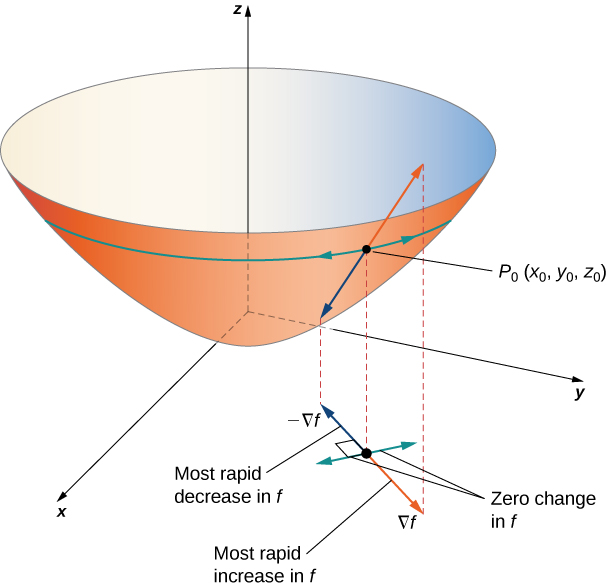
Finding a Maximum Directional Derivative
Find the management for which the directional derivative of ![]() at
at ![]() is a maximum. What is the maximum value?
is a maximum. What is the maximum value?
The maximum value of the directional derivative occurs when ![]() and the unit vector point in the same direction. Therefore, we first past computing
and the unit vector point in the same direction. Therefore, we first past computing ![]()
![]()
Next, nosotros evaluate the slope at ![]()
![]()
We demand to detect a unit of measurement vector that points in the same direction as ![]() and then the adjacent step is to divide
and then the adjacent step is to divide ![]() by its magnitude, which is
by its magnitude, which is ![]() Therefore,
Therefore,
![]()
This is the unit of measurement vector that points in the aforementioned direction equally ![]() To find the bending corresponding to this unit vector, we solve the equations
To find the bending corresponding to this unit vector, we solve the equations
![]()
for ![]() Since cosine is negative and sine is positive, the angle must be in the 2nd quadrant. Therefore,
Since cosine is negative and sine is positive, the angle must be in the 2nd quadrant. Therefore, ![]()
The maximum value of the directional derivative at ![]() is
is ![]() (see the following effigy).
(see the following effigy).
The maximum value of the directional derivative at ![]() is in the direction of the gradient.
is in the direction of the gradient.
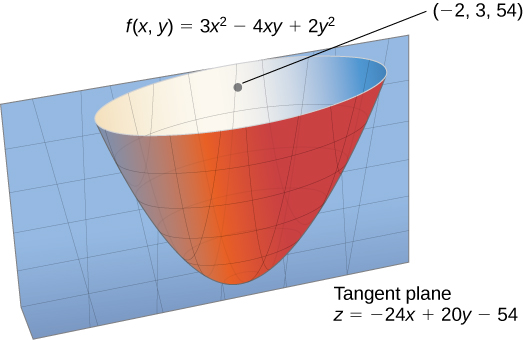
(Figure) shows a portion of the graph of the function ![]() Given a point
Given a point ![]() in the domain of
in the domain of ![]() the maximum value of the gradient at that point is given by
the maximum value of the gradient at that point is given by ![]() This would equal the rate of greatest rising if the surface represented a topographical map. If nosotros went in the opposite direction, it would be the charge per unit of greatest descent.
This would equal the rate of greatest rising if the surface represented a topographical map. If nosotros went in the opposite direction, it would be the charge per unit of greatest descent.
A typical surface in ![]() Given a point on the surface, the directional derivative can be calculated using the gradient.
Given a point on the surface, the directional derivative can be calculated using the gradient.
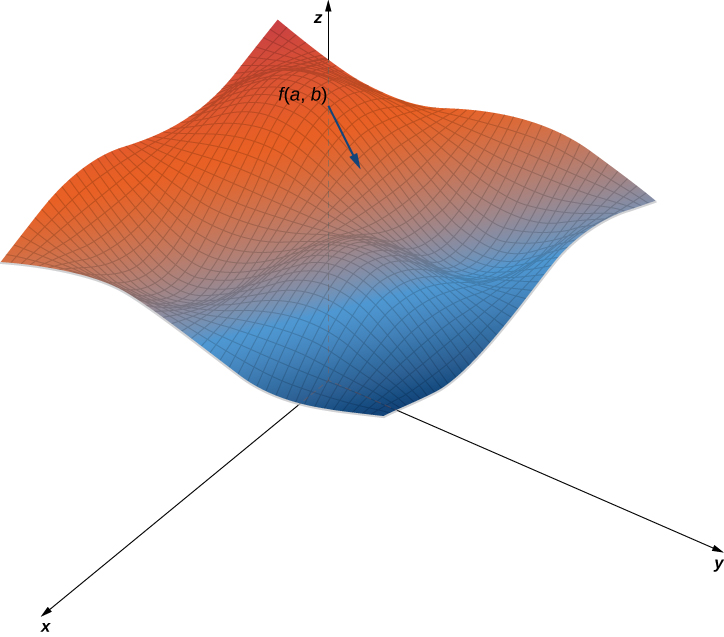
When using a topographical map, the steepest gradient is always in the management where the contour lines are closest together (encounter (Figure)). This is analogous to the contour map of a office, assuming the level curves are obtained for equally spaced values throughout the range of that function.
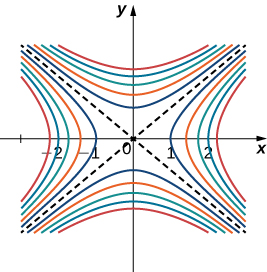
Profile map for the part ![]() using level values between
using level values between ![]() and
and ![]()
Gradients and Level Curves
Recall that if a curve is defined parametrically by the part pair ![]() then the vector
then the vector ![]() is tangent to the curve for every value of
is tangent to the curve for every value of ![]() in the domain. Now let's assume
in the domain. Now let's assume ![]() is a differentiable function of
is a differentiable function of ![]() and
and ![]() is in its domain. Let's suppose farther that
is in its domain. Let's suppose farther that ![]() and
and ![]() for some value of
for some value of ![]() and consider the level bend
and consider the level bend ![]() Define
Define ![]() and calculate
and calculate ![]() on the level bend. Past the chain Rule,
on the level bend. Past the chain Rule,
![]()
But ![]() because
because ![]() for all
for all ![]() Therefore, on the one hand,
Therefore, on the one hand,
![]()
on the other hand,
![]()
Therefore,
![]()
Thus, the dot production of these vectors is equal to zero, which implies they are orthogonal. Still, the 2nd vector is tangent to the level curve, which implies the gradient must exist normal to the level curve, which gives rise to the following theorem.
We tin can utilize this theorem to find tangent and normal vectors to level curves of a role.
Finding Tangents to Level Curves
For the function ![]() find a tangent vector to the level curve at point
find a tangent vector to the level curve at point ![]() Graph the level curve respective to
Graph the level curve respective to ![]() and depict in
and depict in ![]() and a tangent vector.
and a tangent vector.
First, nosotros must calculate ![]()
![]()
Side by side, we evaluate ![]() at
at ![]()
![]()
This vector is orthogonal to the curve at betoken ![]() We tin obtain a tangent vector by reversing the components and multiplying either one by
We tin obtain a tangent vector by reversing the components and multiplying either one by ![]() Thus, for example,
Thus, for example, ![]() is a tangent vector (encounter the post-obit graph).
is a tangent vector (encounter the post-obit graph).
Tangent and normal vectors to ![]() at signal
at signal ![]()
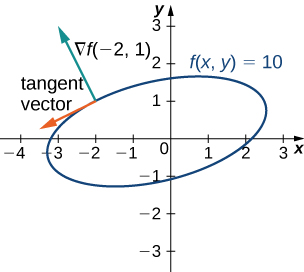
For the function ![]() observe the tangent to the level curve at point
observe the tangent to the level curve at point ![]() Draw the graph of the level curve respective to
Draw the graph of the level curve respective to ![]() and draw
and draw ![]() and a tangent vector.
and a tangent vector.
Hint
Calculate the gradient at point ![]()
Three-Dimensional Gradients and Directional Derivatives
The definition of a gradient tin be extended to functions of more than ii variables.
Definition
Permit ![]() be a function of 3 variables such that
be a function of 3 variables such that ![]() exist. The vector
exist. The vector ![]() is called the gradient of
is called the gradient of ![]() and is defined as
and is defined as
![]()
![]() tin can as well be written as
tin can as well be written as ![]()
Calculating the gradient of a function in three variables is very like to calculating the slope of a function in ii variables. First, we calculate the partial derivatives ![]() and
and ![]() and and so we use (Figure).
and and so we use (Figure).
Finding Gradients in Three Dimensions
Discover the slope ![]() of each of the following functions:
of each of the following functions:
The directional derivative can as well be generalized to functions of three variables. To make up one's mind a direction in three dimensions, a vector with three components is needed. This vector is a unit vector, and the components of the unit of measurement vector are called directional cosines . Given a three-dimensional unit vector ![]() in standard form (i.e., the initial bespeak is at the origin), this vector forms three different angles with the positive
in standard form (i.e., the initial bespeak is at the origin), this vector forms three different angles with the positive ![]() and z-axes. Let's call these angles
and z-axes. Let's call these angles ![]() and
and ![]() And then the directional cosines are given by
And then the directional cosines are given by ![]() and
and ![]() These are the components of the unit vector
These are the components of the unit vector ![]() since
since ![]() is a unit vector, it is truthful that
is a unit vector, it is truthful that ![]()
Definition
Suppose ![]() is a function of 3 variables with a domain of
is a function of 3 variables with a domain of ![]() Permit
Permit ![]() and let
and let ![]() be a unit vector. And then, the directional derivative of
be a unit vector. And then, the directional derivative of ![]() in the direction of
in the direction of ![]() is given by
is given by
![]()
provided the limit exists.
Nosotros tin can calculate the directional derivative of a function of three variables past using the gradient, leading to a formula that is analogous to (Figure).
Directional Derivative of a Function of Three Variables
Let ![]() be a differentiable role of three variables and let
be a differentiable role of three variables and let ![]() be a unit vector. Then, the directional derivative of
be a unit vector. Then, the directional derivative of ![]() in the direction of
in the direction of ![]() is given by
is given by
![]()
The three angles ![]() determine the unit of measurement vector
determine the unit of measurement vector ![]() In practice, we can use an capricious (nonunit) vector, then divide by its magnitude to obtain a unit of measurement vector in the desired direction.
In practice, we can use an capricious (nonunit) vector, then divide by its magnitude to obtain a unit of measurement vector in the desired direction.
Finding a Directional Derivative in Iii Dimensions
Calculate ![]() in the management of
in the management of ![]() for the role
for the role
![]()
Outset, we find the magnitude of ![]()
![]()
Therefore, ![]() is a unit vector in the direction of
is a unit vector in the direction of ![]() and so
and so ![]() Adjacent, nosotros summate the partial derivatives of
Adjacent, nosotros summate the partial derivatives of ![]()
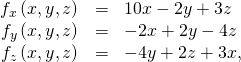
then substitute them into (Figure):
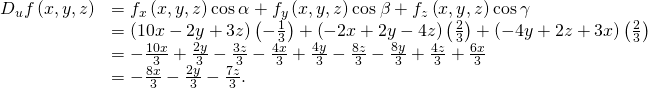
Final, to observe ![]() we substitute
we substitute ![]()
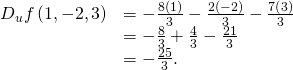
Calculate ![]() and
and ![]() in the direction of
in the direction of ![]() for the function
for the function ![]()
![]()
Hint
First, split up ![]() past its magnitude, calculate the partial derivatives of
past its magnitude, calculate the partial derivatives of ![]() and so utilise (Figure).
and so utilise (Figure).
Key Concepts
- A directional derivative represents a rate of change of a function in any given direction.
- The gradient can be used in a formula to calculate the directional derivative.
- The gradient indicates the direction of greatest change of a function of more than ane variable.
Cardinal Equations
For the following exercises, observe the directional derivative using the limit definition only.
![]() at point
at point ![]() in the management of
in the management of ![]()
![]()
For the following exercises, discover the directional derivative of the function at point ![]() in the management of
in the management of ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For the post-obit exercises, detect the directional derivative of the role in the management of the unit vector ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For the post-obit exercises, find the gradient.
Find the gradient of ![]() And then, find the gradient at bespeak
And then, find the gradient at bespeak ![]()
Observe the slope of ![]() at point
at point ![]()
![]()
![]()
![]()
For the post-obit exercises, notice the directional derivative of the function at point ![]() in the direction of
in the direction of ![]()
![]()
![]()
![]()
For the following exercises, notice the derivative of the function at ![]() in the direction of
in the direction of ![]()
![]()
![]()
![]()
[T] Use technology to sketch the level curve of ![]() that passes through
that passes through ![]() and describe the slope vector at
and describe the slope vector at ![]()
For the following exercises, find the gradient vector at the indicated point.
![]()
![]()
![]()
![]()
![]()
![]()
For the following exercises, detect the derivative of the office.
![]() at point
at point ![]() in the direction the office increases nearly rapidly
in the direction the office increases nearly rapidly
![]() at point
at point ![]() in the direction the role increases about rapidly
in the direction the role increases about rapidly
![]()
![]() at point
at point ![]() in the direction the function increases most rapidly
in the direction the function increases most rapidly
![]() at point
at point ![]() in the management the function increases almost chop-chop
in the management the function increases almost chop-chop
![]()
![]() at point
at point ![]() in the direction the part increases most quickly
in the direction the part increases most quickly
For the post-obit exercises, find the maximum rate of change of ![]() at the given indicate and the direction in which it occurs.
at the given indicate and the direction in which it occurs.
![]()
![]()
![]()
![]()
For the following exercises, discover equations of
- the tangent plane and
- the normal line to the given surface at the given point.
![]() at betoken
at betoken ![]()
For the post-obit exercises, solve the trouble.
Source: https://opentextbc.ca/calculusv3openstax/chapter/directional-derivatives-and-the-gradient/
Posted by: brownwhipeeir.blogspot.com

0 Response to "How To Find Directional Derivative Of A Vector"
Post a Comment