How To Find The Real Zeros Of A Polynomial Function

5.half dozen: Zeros of Polynomial Functions

1. Last updated

2. Salvage as PDF

Page ID

15071

Learning Objectives

• Evaluate a polynomial using the Remainder Theorem.
• Use the Factor Theorem to solve a polynomial equation.
• Use the Rational Zero Theorem to find rational zeros.
• Find zeros of a polynomial office.
• Utilize the Linear Factorization Theorem to detect polynomials with given zeros.
• Use Descartes' Rule of Signs.
• Solve real-globe applications of polynomial equations

A new baker offers decorated sheet cakes for children's birthday parties and other special occasions. The bakery wants the volume of a small-scale cake to be 351 cubic inches. The block is in the shape of a rectangular solid. They want the length of the cake to be iv inches longer than the width of the cake and the pinnacle of the cake to be one-third of the width. What should the dimensions of the cake pan be?

This problem tin can be solved by writing a cubic function and solving a cubic equation for the volume of the cake. In this section, we will hash out a variety of tools for writing polynomial functions and solving polynomial equations.

Evaluating a Polynomial Using the Residual Theorem

In the final section, we learned how to divide polynomials. We can now use polynomial division to evaluate polynomials using the Residue Theorem. If the polynomial is divided by \(x–thousand\), the remainder may be found chop-chop past evaluating the polynomial office at \(k\), that is, \(f(grand)\). Permit's walk through the proof of the theorem.

Recall that the Division Algorithm states that, given a polynomial dividend \(f(x)\) and a not-zero polynomial divisor \(d(x)\) where the caste of \(d(ten)\) is less than or equal to the degree of \(f(x)\),there be unique polynomials \(q(10)\) and \(r(x)\) such that

\[f(10)=d(x)q(x)+r(x) \nonumber\]

If the divisor, \(d(ten)\), is \(x−k\), this takes the form

\[f(x)=(ten−grand)q(x)+r \nonumber\]

Since the divisor \(ten−grand\)

is linear, the residuum will be a constant, \(r\). And, if we evaluate this for \(x=k\), we accept

\[\begin{marshal*} f(grand)&=(grand−k)q(m)+r \\[4pt] &=0{\cdot}q(one thousand)+r \\[4pt] &=r \end{align*}\]

In other words, \(f(k)\) is the remainder obtained by dividing \(f(x)\)by \(x−k\).

The Rest Theorem

If a polynomial \(f(x)\) is divided by \(x−one thousand\),and then the remainder is the value \(f(k)\).

Given a polynomial function \(f\), evaluate \(f(ten)\) at \(x=k\) using the Remainder Theorem.

1. Use synthetic sectionalization to divide the polynomial by \(x−thousand\).
2. The remainder is the value \(f(k)\).

Case \(\PageIndex{1}\): Using the Remainder Theorem to Evaluate a Polynomial

Use the Residue Theorem to evaluate \(f(x)=6x^4−ten^3−15x^2+2x−seven\) at \(x=2\).

Solution

To find the rest using the Remainder Theorem, employ synthetic segmentation to dissever the polynomial past \(10−2\).

\[ two \begin{array}{|ccccc} \; 6 & −1 & −xv & 2 & −7 \\ \text{} & 12 & 22 & fourteen & 32 \\ \hline \end{array} \\ \begin{array}{ccccc} 6 & 11 & \; 7 & \;\;16 & \;\; 25 \end{array} \]

The remainder is 25. Therefore, \(f(two)=25\).

Assay

We tin can check our respond past evaluating \(f(ii)\).

\[\brainstorm{marshal*} f(x)&=6x^4−x^iii−15x^2+2x−vii \\ f(ii)&=six(ii)^4−(2)^3−xv(ii)^2+2(ii)−7 \\ &=25 \finish{align*}\]

Exercise \(\PageIndex{1}\)

se the Balance Theorem to evaluate \(f(x)=2x^5−3x^iv−9x^3+8x^2+2\) at \(x=−three\).

Respond

\(f(−3)=−412\)

Using the Gene Theorem to Solve a Polynomial Equation

The Factor Theorem is another theorem that helps us clarify polynomial equations. It tells us how the zeros of a polynomial are related to the factors. Recall that the Segmentation Algorithm.

\[f(x)=(x−k)q(x)+r\]

If \(k\) is a nil, so the remainder \(r\) is \(f(k)=0\) and \(f (x)=(x−k)q(x)+0\) or \(f(x)=(x−k)q(x)\).

Find, written in this course, \(x−k\) is a factor of \(f(10)\). We can conclude if \(1000\) is a zippo of \(f(x)\), then \(ten−k\) is a factor of \(f(x)\).

Similarly, if \(ten−k\) is a factor of \(f(x)\), then the remainder of the Partition Algorithm \(f(10)=(x−k)q(x)+r\) is \(0\). This tells united states of america that \(grand\) is a zip.

This pair of implications is the Factor Theorem. As we volition presently see, a polynomial of degree \(n\) in the circuitous number system will have \(n\) zeros. Nosotros can use the Factor Theorem to completely factor a polynomial into the product of \(north\) factors. One time the polynomial has been completely factored, we can easily determine the zeros of the polynomial.

THE FACTOR THEOREM

According to the Factor Theorem, \(k\) is a zero of \(f(ten)\) if and only if \((x−k)\) is a factor of \(f(x)\).

How to: Given a factor and a third-caste polynomial, use the Factor Theorem to factor the polynomial

1. Utilise synthetic division to split up the polynomial by \((10−1000)\).
2. Confirm that the remainder is \(0\).
3. Write the polynomial as the product of \((x−m)\) and the quadratic quotient.
4. If possible, gene the quadratic.
5. Write the polynomial as the product of factors.

Example \(\PageIndex{ii}\): Using the Factor Theorem to Solve a Polynomial Equation

Show that \((10+2)\) is a factor of \(ten^3−6x^ii−x+xxx\). Find the remaining factors. Use the factors to determine the zeros of the polynomial.

Solution

We can use synthetic division to bear witness that \((10+ii)\) is a factor of the polynomial.

\[ -2 \begin{array}{|cccc} \; ane & −6 & −i & 30 \\ \text{} & -two & xvi & -30 \\ \hline \finish{array} \\ \brainstorm{assortment}{cccc} 1 & -eight & \; 15 & \;\;0 \end{array} \]

The balance is zilch, then \((x+2)\) is a cistron of the polynomial. We can use the Partitioning Algorithm to write the polynomial as the production of the divisor and the caliber:

\[(ten+ii)(x^ii−8x+fifteen)\]

We can factor the quadratic factor to write the polynomial as

\[(x+two)(ten−3)(x−5)\]

Past the Factor Theorem, the zeros of \(x^three−6x^2−x+30\) are –2, 3, and five.

Exercise \(\PageIndex{2}\)

Employ the Factor Theorem to find the zeros of \(f(x)=x^iii+4x^two−4x−16\) given that \((x−2)\) is a cistron of the polynomial.

Answer

The zeros are ii, –2, and –4.

Using the Rational Zippo Theorem to Observe Rational Zeros

Another utilise for the Remainder Theorem is to test whether a rational number is a nil for a given polynomial. Simply offset we need a pool of rational numbers to test. The Rational Cypher Theorem helps us to narrow down the number of possible rational zeros using the ratio of the factors of the constant term and factors of the leading coefficient of the polynomial

Consider a quadratic role with two zeros, \(x=\frac{2}{5}\) and \(x=\frac{3}{iv}\). By the Factor Theorem, these zeros have factors associated with them. Let u.s. set each factor equal to 0, and then construct the original quadratic function absent its stretching factor.

Detect that ii of the factors of the abiding term, 6, are the ii numerators from the original rational roots: 2 and 3. Similarly, 2 of the factors from the leading coefficient, xx, are the two denominators from the original rational roots: 5 and 4.

We tin infer that the numerators of the rational roots will always be factors of the constant term and the denominators volition be factors of the leading coefficient. This is the essence of the Rational Zilch Theorem; it is a means to requite us a pool of possible rational zeros.

THE RATIONAL Naught THEOREM

The Rational Null Theorem states that, if the polynomial \(f(x)=a_nx^n+a_{northward−ane}x^{n−one}+...+a_1x+a_0\) has integer coefficients, then every rational zip of \(f(x)\) has the form \(\frac{p}{q}\) where \(p\) is a factor of the constant term \(a_0\) and \(q\) is a cistron of the leading coefficient \(a_n\).

When the leading coefficient is 1, the possible rational zeros are the factors of the constant term.

How to: Given a polynomial office \(f(x)\), employ the Rational Zippo Theorem to observe rational zeros.

1. Decide all factors of the constant term and all factors of the leading coefficient.
2. Determine all possible values of \(\dfrac{p}{q}\), where \(p\) is a gene of the constant term and \(q\) is a cistron of the leading coefficient. Be certain to include both positive and negative candidates.
3. Determine which possible zeros are actual zeros by evaluating each case of \(f(\frac{p}{q})\).

Example \(\PageIndex{3}\): List All Possible Rational Zeros

Listing all possible rational zeros of \(f(10)=2x^4−5x^three+x^2−4\).

Solution

The only possible rational zeros of \(f(ten)\) are the quotients of the factors of the last term, –4, and the factors of the leading coefficient, 2.

The constant term is –4; the factors of –4 are \(p=±one,±2,±iv\).

The leading coefficient is 2; the factors of ii are \(q=±1,±2\).

If whatsoever of the four real zeros are rational zeros, so they will be of 1 of the post-obit factors of –4 divided past one of the factors of two.

\[\dfrac{p}{q}=±\dfrac{1}{ane},±\dfrac{1}{ii} \; \; \; \; \; \; \frac{p}{q}=±\dfrac{2}{1},±\dfrac{2}{2} \; \; \; \; \; \; \dfrac{p}{q}=±\dfrac{4}{1},±\dfrac{iv}{2} \nonumber\]

Note that \(\frac{2}{2}=i\) and \(\frac{iv}{ii}=ii\), which have already been listed. And then nosotros can shorten our list.

\[\dfrac{p}{q} = \dfrac{\text{Factors of the last}}{\text{Factors of the first}}=±1,±ii,±four,±\dfrac{1}{two}\nonumber \]

Example \(\PageIndex{4}\): Using the Rational Zero Theorem to Find Rational Zeros

Utilize the Rational Aught Theorem to find the rational zeros of \(f(ten)=2x^iii+x^2−4x+ane\).

Solution

The Rational Zero Theorem tells us that if \(\frac{p}{q}\) is a zero of \(f(10)\), and so \(p\) is a factor of one and \(q\) is a factor of 2.

\[ \begin{marshal*} \dfrac{p}{q}=\dfrac{factor\infinite of\space constant\space term}{factor\space of\space leading\infinite coefficient} \\[4pt] &=\dfrac{factor\infinite of\space 1}{factor\space of\space 2} \cease{align*}\]

The factors of 1 are ±1 and the factors of 2 are ±1 and ±2. The possible values for \(\frac{p}{q}\) are ±ane and \(±\frac{one}{two}\). These are the possible rational zeros for the function. We can make up one's mind which of the possible zeros are actual zeros by substituting these values for \(10\) in \(f(x)\).

\[f(−one)=2{(−i)}^3+{(−i)}^2−4(−1)+one=4\]

\[f(1)=1{(1)}^three+{(1)}^2−four(ane)+1=0\]

\[f(−\dfrac{one}{2})=two{(−\dfrac{1}{two})}^3+{(−\dfrac{1}{ii})}^ii−4(−\dfrac{i}{2})+1=three\]

\[f(\dfrac{1}{two})=2{(\dfrac{ane}{2})}^3+{(\dfrac{1}{2})}^ii−4(\dfrac{1}{two})+1=−\dfrac{one}{two}\]

Of those, \(−1\),\(−\dfrac{ane}{two}\), and \(\dfrac{1}{2}\) are not zeros of \(f(ten)\). 1 is the only rational nothing of \(f(x)\).

Practice \(\PageIndex{3}\)

Use the Rational Zero Theorem to find the rational zeros of \(f(x)=x^three−5x^2+2x+1\).

Answer

There are no rational zeros.

Finding the Zeros of Polynomial Functions

The Rational Zero Theorem helps the states to narrow down the list of possible rational zeros for a polynomial office. Once nosotros take done this, nosotros can apply synthetic division repeatedly to determine all of the zeros of a polynomial function.

How to: Given a polynomial role \(f\), use synthetic partitioning to find its zeros.

1. Use the Rational Zippo Theorem to listing all possible rational zeros of the function.
2. Employ constructed division to evaluate a given possible nil past synthetically dividing the candidate into the polynomial. If the residue is 0, the candidate is a zero. If the remainder is not cipher, discard the candidate.
3. Repeat step ii using the quotient found with constructed division. If possible, continue until the quotient is a quadratic.
4. Find the zeros of the quadratic function. Two possible methods for solving quadratics are factoring and using the quadratic formula.

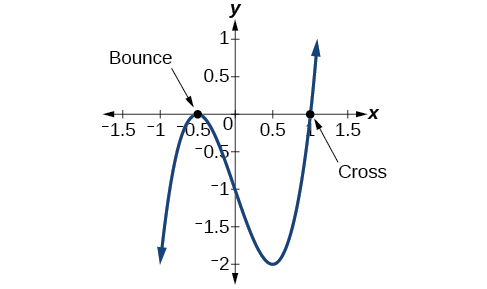
Example \(\PageIndex{5}\): Finding the Zeros of a Polynomial Function with Repeated Existent Zeros

Find the zeros of \(f(x)=4x^three−3x−1\).

Solution

The Rational Zero Theorem tells united states that if \(\dfrac{p}{q}\) is a zero of \(f(x)\), so \(p\) is a cistron of –1 and \(q\) is a cistron of 4.

\[\begin{align*}\dfrac{p}{q}=\dfrac{factor\space of\space abiding\infinite term}{gene\space of\space leading\infinite coefficient} \\[4pt] =\dfrac{cistron\space of\space -1}{factor\space of\infinite iv} \end{align*}\]

The factors of –ane are ±1 and the factors of iv are ±1,±ii, and ±4. The possible values for \(\dfrac{p}{q}\) are \(±1\),\(±\dfrac{1}{two}\), and \(±\dfrac{1}{4}\). These are the possible rational zeros for the function. We will use constructed sectionalisation to evaluate each possible zero until nosotros find one that gives a residual of 0. Let's begin with one.

Dividing by \((x−1)\) gives a balance of 0, so ane is a zero of the function. The polynomial tin exist written as

\[(10−ane)(4x^2+4x+1) \nonumber\]

The quadratic is a perfect square. \(f(x)\) tin be written as

\[(x−i){(2x+1)}^2\nonumber\]

We already know that i is a zero. The other zero will have a multiplicity of 2 because the factor is squared. To find the other zero, we tin can set the gene equal to 0.

\[ \brainstorm{align*} 2x+one=0 \\[4pt] x &=−\dfrac{1}{2} \terminate{align*}\]

The zeros of the function are 1 and \(−\frac{ane}{two}\) with multiplicity 2.

Analysis

Look at the graph of the part \(f\) in Effigy \(\PageIndex{one}\). Detect, at \(ten =−0.5\), the graph bounces off the x-axis, indicating the even multiplicity (2,iv,6…) for the zero −0.5. At \(x=1\), the graph crosses the x-centrality, indicating the odd multiplicity (i,three,v…) for the zero \(ten=one\).

Figure \(\PageIndex{ane}\).

Using the Fundamental Theorem of Algebra

At present that we can observe rational zeros for a polynomial function, we volition look at a theorem that discusses the number of complex zeros of a polynomial role. The Fundamental Theorem of Algebra tells us that every polynomial function has at to the lowest degree 1 complex nil. This theorem forms the foundation for solving polynomial equations.

Suppose \(f\) is a polynomial function of degree iv, and \(f (x)=0\). The Primal Theorem of Algebra states that there is at least i complex solution, call it \(c_1\). By the Factor Theorem, we can write \(f(x)\) as a product of \(x−c_1\) and a polynomial quotient. Since \(x−c_1\) is linear, the polynomial quotient will exist of degree three. Now we apply the Fundamental Theorem of Algebra to the third-degree polynomial caliber. It will have at least one complex zero, telephone call it \(c_2\). So we can write the polynomial quotient as a product of \(10−c_2\) and a new polynomial quotient of caste two. Keep to apply the Fundamental Theorem of Algebra until all of the zeros are found. At that place volition be 4 of them and each i will yield a factor of \(f(ten)\).

THE FUNDAMENTAL THEOREM OF ALGEBRA

The Fundamental Theorem of Algebra states that, if \(f(x)\) is a polynomial of degree \(north > 0\), then \(f(x)\) has at least one complex zero.

We can apply this theorem to argue that, if \(f(ten)\) is a polynomial of caste \(n >0\), and a is a non-zero real number, then \(f(x)\) has exactly \(n\) linear factors

\[f(10)=a(x−c_1)(10−c_2)...(10−c_n)\]

where \(c_1,c_2\),...,\(c_n\) are complex numbers. Therefore, \(f(10)\) has \(northward\) roots if we let for multiplicities.

Q&A: Does every polynomial have at to the lowest degree one imaginary zilch?

No. Existent numbers are a subset of complex numbers, but not the other way around. A complex number is non necessarily imaginary. Real numbers are too complex numbers.

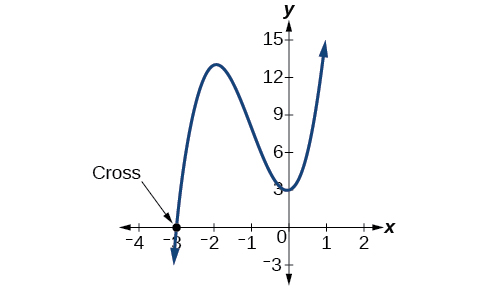
Example \(\PageIndex{vi}\): Finding the Zeros of a Polynomial Function with Complex Zeros

Discover the zeros of \(f(10)=3x^3+9x^2+x+iii\).

Solution

The Rational Zero Theorem tells u.s.a. that if \(\frac{p}{q}\) is a zero of \(f(x)\), and so \(p\) is a factor of 3 and \(q\) is a gene of iii.

\[ \brainstorm{align*} \dfrac{p}{q}=\dfrac{factor\infinite of\space constant\space term}{factor\infinite of\space leading\space coefficient} \\[4pt] &=\dfrac{factor\space of\space three}{gene\space of\space three} \terminate{align*}\]

The factors of three are ±1 and ±iii. The possible values for \(\dfrac{p}{q}\), and therefore the possible rational zeros for the function, are ±3,±one, and \(±\dfrac{ane}{3}\). We volition use constructed division to evaluate each possible naught until we find i that gives a remainder of 0. Let's begin with –3.

Dividing by \((10+3)\) gives a remainder of 0, then –3 is a zero of the role. The polynomial tin can be written as

\[(x+3)(3x^2+1) \nonumber\]

We can and then ready the quadratic equal to 0 and solve to find the other zeros of the function.

\[ \begin{align*} 3x^two+1=0 \\[4pt] x^2 &=−\dfrac{1}{3} \\[4pt] ten&=±−\sqrt{\dfrac{one}{3}} \\[4pt] &=±\dfrac{i\sqrt{3}}{iii} \end{align*}\]

The zeros of \(f(x)\) are \(–3\) and \(±\dfrac{i\sqrt{3}}{3}\).

Analysis

Look at the graph of the function \(f\) in Effigy \(\PageIndex{2}\). Detect that, at \(x =−3\), the graph crosses the x-centrality, indicating an odd multiplicity (1) for the zippo \(x=–3\). Also annotation the presence of the two turning points. This means that, since there is a \(3^{rd}\) degree polynomial, we are looking at the maximum number of turning points. So, the end behavior of increasing without leap to the right and decreasing without spring to the left will proceed. Thus, all the x-intercepts for the role are shown. So either the multiplicity of \(x=−3\) is one and in that location are two circuitous solutions, which is what we found, or the multiplicity at \(10 =−3\) is three. Either way, our result is correct.

Figure \(\PageIndex{two}\).

\(\PageIndex{4}\)

Find the zeros of \(f(10)=2x^3+5x^ii−11x+4\).

Solution

The zeros are \(–4\), \(\frac{1}{2}\), and \(1\).

Using the Linear Factorization Theorem to Discover Polynomials with Given Zeros

A vital implication of the Fundamental Theorem of Algebra, every bit we stated higher up, is that a polynomial part of degree n will take \(n\) zeros in the set of circuitous numbers, if we allow for multiplicities. This means that we can factor the polynomial function into \(n\) factors. The Linear Factorization Theorem tells united states of america that a polynomial function will take the same number of factors equally its degree, and that each factor will exist in the form \((x−c)\), where c is a complex number.

Let \(f\) exist a polynomial function with real coefficients, and suppose \(a +bi\), \(b≠0\), is a zero of \(f(x)\). Then, by the Cistron Theorem, \(x−(a+bi)\) is a factor of \(f(10)\). For \(f\) to have real coefficients, \(ten−(a−bi)\) must besides exist a factor of \(f(ten)\). This is true because whatsoever factor other than \(x−(a−bi)\), when multiplied past \(ten−(a+bi)\), will leave imaginary components in the product. Just multiplication with conjugate pairs will eliminate the imaginary parts and effect in existent coefficients. In other words, if a polynomial office \(f\) with real coefficients has a complex zero \(a +bi\), then the complex conjugate \(a−bi\) must besides be a zero of \(f(x)\). This is called the Complex Conjugate Theorem.

Circuitous CONJUGATE THEOREM

According to the Linear Factorization Theorem, a polynomial role will have the same number of factors every bit its degree, and each gene will be in the grade \((x−c)\), where \(c\) is a complex number.

If the polynomial role \(f\) has existent coefficients and a complex zero in the class \(a+bi\), then the complex cohabit of the zero, \(a−bi\), is also a zero.

How to

Given the zeros of a polynomial office \(f\) and a point \((c, f(c))\) on the graph of \(f\), use the Linear Factorization Theorem to detect the polynomial function.

1. Use the zeros to construct the linear factors of the polynomial.
2. Multiply the linear factors to expand the polynomial.
3. Substitute \((c,f(c))\) into the function to make up one's mind the leading coefficient.
4. Simplify.

Example \(\PageIndex{7}\): Using the Linear Factorization Theorem to Find a Polynomial with Given Zeros

Notice a fourth caste polynomial with existent coefficients that has zeros of \(–iii\), \(two\), \(i\), such that \(f(−2)=100\).

Solution

Considering \(ten =i\) is a aught, by the Complex Conjugate Theorem \(x =–i\) is also a goose egg. The polynomial must have factors of \((10+3),(ten−ii),(x−i)\), and \((x+i)\). Since we are looking for a degree 4 polynomial, and at present take four zeros, we have all four factors. Let's begin by multiplying these factors.

\[\brainstorm{marshal} f(x) & =a(x+iii)(ten−2)(x−i)(10+i) \\ f(x) & =a(x^2+10−half-dozen)(x^2+1) \\ f(x) & =a(x^4+x^iii−5x^ii+x−6) \cease{align} \]

We need to find \(a\) to ensure \(f(–ii)=100\). Substitute \(ten=–2\) and \(f (-2)=100\) into \(f (x)\).

\[\begin{align} 100=a({(−2)}^four+{(−2)}^3−5{(−2)}^2+(−2)−half-dozen) \\ 100=a(−20) \\ −5=a \end{marshal} \]

So the polynomial role is

\[f(x)=−5(x^4+10^3−5x^ii+10−6)\]

or

\[f(x)=−5x^4−5x^3+25x^2−5x+30\] Assay

Nosotros found that both \(i\) and \(−i\) were zeros, just but one of these zeros needed to be given. If \(i\) is a cipher of a polynomial with real coefficients, then \(−i\) must as well be a zero of the polynomial because \(−i\) is the circuitous conjugate of \(i\).

Q&A

If \(two+3i\) were given as a nil of a polynomial with existent coefficients, would \(ii−3i\) besides demand to exist a cipher?

Yes. When any complex number with an imaginary component is given as a zippo of a polynomial with real coefficients, the cohabit must likewise be a zippo of the polynomial.

\(\PageIndex{5}\)

Detect a third degree polynomial with real coefficients that has zeros of \(v\) and \(−2i\) such that \(f (1)=10\).

Solution

\(f(x)=−\frac{1}{2}x^3+\frac{5}{2}x^2−2x+x\)

Using Descartes' Dominion of Signs

There is a straightforward way to determine the possible numbers of positive and negative real zeros for any polynomial office. If the polynomial is written in descending order, Descartes' Rule of Signs tells us of a relationship between the number of sign changes in \(f(x)\) and the number of positive real zeros. For example, the polynomial function beneath has i sign alter.

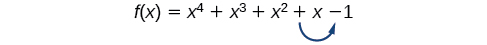
This tells us that the role must have one positive real zero.

At that place is a like relationship betwixt the number of sign changes in \(f(−x)\) and the number of negative existent zeros.

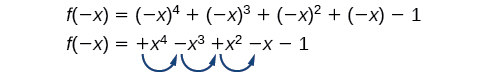
In this case, \(f(−x)\) has 3 sign changes. This tells us that \(f(x)\) could take 3 or 1 negative real zeros.

DESCARTES' RULE OF SIGNS

According to Descartes' Dominion of Signs, if we let \(f(10)=a_nx^n+a_{n−1}x^{n−1}+...+a_1x+a_0\) exist a polynomial function with real coefficients:

• The number of positive real zeros is either equal to the number of sign changes of \(f(10)\) or is less than the number of sign changes past an even integer.
• The number of negative real zeros is either equal to the number of sign changes of \(f(−x)\) or is less than the number of sign changes past an even integer.

Example \(\PageIndex{8}\): Using Descartes' Rule of Signs

Apply Descartes' Rule of Signs to make up one's mind the possible numbers of positive and negative existent zeros for \(f(10)=−x^4−3x^3+6x^2−4x−12\).

Solution

Begin by determining the number of sign changes.

There are two sign changes, so at that place are either 2 or 0 positive real roots. Next, we examine \(f(−x)\) to determine the number of negative existent roots.

\[ \begin{align} f(−x) & =−{(−x)}^iv−3{(−x)}^3+6{(−x)}^2−4(−ten)−12 \\ f(−x) & =−10^4+3x^3+6x^2+4x−12 \end{align} \]

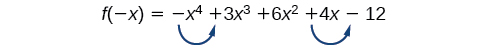
Again, there are two sign changes, so at that place are either two or 0 negative existent roots.

There are four possibilities, as nosotros can run into in Tabular array \(\PageIndex{1}\).

Table \(\PageIndex{one}\)

Positive Real Zeros	Negative Real Zeros	Complex Zeros	Total Zeros
2	two	0	4
2	0	2	four
0	two	2	4
0	0	iv	4

Analysis

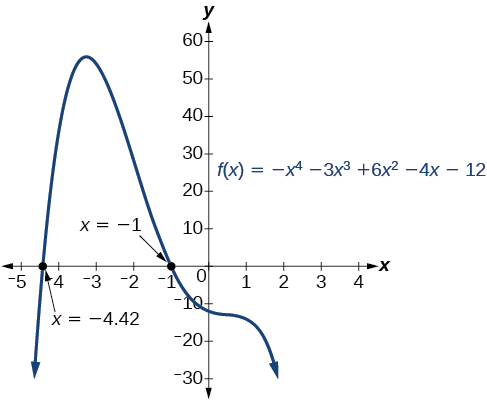
We tin ostend the numbers of positive and negative real roots by examining a graph of the function. See Figure \(\PageIndex{3}\). We can encounter from the graph that the function has 0 positive real roots and two negative real roots.

Figure \(\PageIndex{3}\).

\(\PageIndex{half dozen}\)

Apply Descartes' Rule of Signs to determine the maximum possible numbers of positive and negative real zeros for \(f(x)=2x^4−10x^3+11x^2−15x+12\). Use a graph to verify the numbers of positive and negative real zeros for the part.

Solution

At that place must exist four, 2, or 0 positive real roots and 0 negative real roots. The graph shows that there are two positive real zeros and 0 negative real zeros.

Solving Real-World Applications

We have now introduced a diversity of tools for solving polynomial equations. Let's use these tools to solve the bakery problem from the beginning of the section.

Instance \(\PageIndex{9}\)

Solving Polynomial Equations

A new bakery offers decorated sheet cakes for children's altogether parties and other special occasions. The bakery wants the volume of a small block to be 351 cubic inches. The cake is in the shape of a rectangular solid. They want the length of the cake to be iv inches longer than the width of the cake and the pinnacle of the cake to be one-tertiary of the width. What should the dimensions of the block pan be?

Solution

Begin by writing an equation for the volume of the block. The book of a rectangular solid is given by \(V=lwh\). We were given that the length must be four inches longer than the width, so we tin can limited the length of the cake as \(fifty=westward+iv\). Nosotros were given that the peak of the block is i-third of the width, so we can express the height of the cake as \(h=\dfrac{one}{3}w\). Let'southward write the volume of the block in terms of width of the cake.

\[V=(westward+iv)(w)(\dfrac{1}{3}west)\] \[5=\dfrac{1}{3}w^3+\dfrac{iv}{3}w^2\]

Substitute the given volume into this equation.

\(351=13w^3+43w^2\) Substitute 351 for V. \(1053=due west^three+4w^2\) Multiply both sides by three. \(0=w^3+7w^2−1053\) Subtract 1053 from both sides.

Descartes' rule of signs tells us there is one positive solution. The Rational Zero Theorem tells usa that the possible rational zeros are \(\pm i,±3,±9,±13,±27,±39,±81,±117,±351,\) and \(±1053\). We can use constructed sectionalization to test these possible zeros. Only positive numbers make sense equally dimensions for a cake, so we need non exam any negative values. Permit's begin by testing values that make the most sense equally dimensions for a pocket-size sheet cake. Use synthetic partitioning to check \(x=1\).

Since ane is not a solution, we will check \(10=three\).

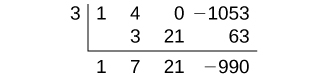
Since 3 is non a solution either, we will test \(x=nine\).

Constructed division gives a remainder of 0, so 9 is a solution to the equation. We can use the relationships between the width and the other dimensions to determine the length and height of the sheet cake pan.

\(l=w+four=9+4=13\) and \(h=\dfrac{1}{3}westward=\dfrac{1}{3}(9)=iii\)

The canvas cake pan should have dimensions 13 inches by ix inches by 3 inches

\(\PageIndex{7}\)

A aircraft container in the shape of a rectangular solid must have a volume of 84 cubic meters. The customer tells the manufacturer that, considering of the contents, the length of the container must be one meter longer than the width, and the acme must exist one meter greater than twice the width. What should the dimensions of the container exist?

Solution

3 meters by four meters by seven meters

Central Concepts

• To detect \(f(thousand)\), determine the remainder of the polynomial \(f(x)\) when it is divided by \(10−one thousand\). This is known every bit the Residue Theorem. See Instance \(\PageIndex{i}\).
• According to the Cistron Theorem, \(thousand\) is a zero of \(f(x)\) if and but if \((x−k)\) is a factor of \(f(x)\). Come across Case\(\PageIndex{2}\).
• According to the Rational Zero Theorem, each rational zero of a polynomial function with integer coefficients will be equal to a gene of the constant term divided by a gene of the leading coefficient. Run across Example \(\PageIndex{3}\) and Example \(\PageIndex{four}\).
• When the leading coefficient is 1, the possible rational zeros are the factors of the constant term.
• Constructed sectionalization tin be used to notice the zeros of a polynomial office. Meet Instance \(\PageIndex{5}\).
• Co-ordinate to the Fundamental Theorem, every polynomial part with degree greater than 0 has at least one complex zip. See Instance \(\PageIndex{half-dozen}\).
• Allowing for multiplicities, a polynomial part volition accept the same number of factors equally its degree. Each factor will exist in the form \((x−c)\), where \(c\) is a complex number. See Example \(\PageIndex{7}\).
• The number of positive existent zeros of a polynomial office is either the number of sign changes of the part or less than the number of sign changes by an even integer.
• The number of negative existent zeros of a polynomial function is either the number of sign changes of \(f(−x)\) or less than the number of sign changes by an even integer. Encounter Case \(\PageIndex{8}\).
• Polynomial equations model many real-world scenarios. Solving the equations is easiest done by synthetic partition. See Example \(\PageIndex{nine}\).

Glossary

Descartes' Rule of Signs

a dominion that determines the maximum possible numbers of positive and negative real zeros based on the number of sign changes of \(f(x)\) and \(f(−x)\)

Gene Theorem

\(k\) is a aught of polynomial function \(f(10)\) if and only if \((x−thou)\) is a gene of \(f(x)\)

Primal Theorem of Algebra

a polynomial role with degree greater than 0 has at to the lowest degree one complex null

Linear Factorization Theorem

allowing for multiplicities, a polynomial role will have the same number of factors equally its degree, and each gene will be in the form \((ten−c)\), where \(c\) is a complex number

Rational Goose egg Theorem

the possible rational zeros of a polynomial office have the form \(\frac{p}{q}\) where \(p\) is a cistron of the constant term and \(q\) is a factor of the leading coefficient.

Residual Theorem

if a polynomial \(f(x)\) is divided by \(x−k\),then the remainder is equal to the value \(f(1000)\)

Source: https://math.libretexts.org/Bookshelves/Algebra/Map%3A_College_Algebra_(OpenStax)/05%3A_Polynomial_and_Rational_Functions/506%3A_Zeros_of_Polynomial_Functions

Posted by: brownwhipeeir.blogspot.com

Share this post